Poliedros compuestos
Poliedro compuesto es aquel que está formado por varios poliedros que comparten un centro en común.
Decimos que es un politopo compuesto la figura formada por varios politopos con centro común, si tienen dos dimensiones se llaman compuestos poligonales mientras que si tienen tres dimensiones se llaman poliedros compuestos.
Los vértices externos de un poliedro compuesto se pueden unir para formar un politopo convexo, es lo que se llama un envolvente convexo.
Se pueden generar compuestos poliédricos regulares a partir de los cinco poliedros regulares
Tenemos como ejemplo la estrella octángula formada por dos tetraedros, los vértices de esta figura definen un cubo y el sólido de intersección es un octaedro regular pues comparte realmente los mismos planos que definen las caras del compuesto poliédrico.
Aquellos poliedros compuestos que están formados por un poliedro y su dual se llaman poliedros compuestos duales, tenemos en este caso los dos tetraedros regulares entrelazados o estrella octángula, ya que el tetraedro regular es dual de sí mismo, luego tenemos la composición de cubo y octaedro, cuya intersección genera el cuboctaedro.
Luego tenemos la composición del dodecaedro e icosaedro y cuya intersección produce el icosidodecaedro.
Tenemos luego la intersección del gran icosaedro y del gran dodecaedro estrellado y cuya intersección produce también el icosidodecaedro y por último tenemos que el pequeño dodecaedro estrellado compuesto con el gran dodecaedro produce en su intersección el dodecaedro regular.
Los vértices de esos cinco poliedros compuestos duales provocan respectivamente las siguientes figuras:
El cubo, -el rombododecaedro, el triacontaedro rómbico- (2 poliedros de Catalan), el dodecaedro y el icosaedro, eso quiere decir que si por ejemplo cogemos la primera figura que está compuesta por dos tetraedros regulares al tomar sus vértices externos vemos que pasan o coinciden con los vértices de un cubo, si cogemos la segunda figura, la intersección del octaedro y del cubo vemos que los vértices externos de ambas figuras producen el rombododecaedro y así con los otros 3.
Se pueden generar infinitas variedades de poliedros compuestos por ejemplo el conocido de 3 octaedros o el de 4 cubos, también se pueden generar a partir de la intersección de varios poliedros o de intersección de poliedros con otras superficies, como por ejemplo los que se muestran al final de este blog o en https://interseccion-de-cuerpos.blogspot.com/.
En la figura 1 vemos dos prismas rectos de sección en rombo, el rombo no está formado por 2 triángulos equiláteros como puede parecer. La intersección de los dos prismas nos provoca la figura número 3 que es un octaedro regular, en el que las tres medidas de los ejes opuestos que pasan por los vértices son iguales.
En el número 2 hemos puesto en planta y alzado el mismo octaedro regular pero hemos incorporado un cubo para que se vea la relación entre las medidas de las aristas de las figuras, como podemos observar en esta proyección dos vértices del cubo coinciden con 2 vértices del octaedro regular.
En la figura 4 aparece nuevamente el octaedro regular en sistema diédrico, en la 5 tenemos el cubo en planta y alzado, en las 6 tenemos las dos figuras anteriores superpuestas y con el centro común, es lo que se llama un poliedro compuesto, en este caso del cubo y del octaedro regular.
En la figura 7 obtenemos la intersección de los 2 poliedros, se obtiene un cuboctaedro que es un poliedro arquimediano que también lo podemos obtener al coger un cubo y cortar sus 8 esquinas por planos que pasen por la mitad de las aristas, por tanto será una figura formada por 6 cuadrados laterales y 8 triángulos o bases de las pirámides que se le quitan. Si cogemos la figura 6 en planta y alzado y la vemos en el espacio, como por ejemplo en la figura 19, al marcar los puntos que aparecen en color negro correspondientes a las 2 figuras, obtenemos los puntos del rombododecaedro que aparece en la Figura 18, es lo que se llama la figura envolvente convexa de un poliedro compuesto, si nos fijamos hemos cogido todos los vértices externos para componer en este caso un poliedro de Catalan; los poliedros de catalán son duales de los arquimedianos y están formados por caras iguales. Si cogemos los puntos medios de las caras de un poliedro de Catalan obtenemos un poliedro arquimediano, la recíproca no es cierta.
Eso quiere decir que si cogemos el rombododecaedro, figura número 17, y cogemos los puntos medios de sus caras obtenemos el cuboctaedro que es la figura 16 y a la que se llama núcleo por ser la intersección de los 2 poliedros que forman el poliedro compuesto.
El cubo y octaedro regular son poliedros regulares y por tanto tienen las caras que son polígonos regulares, son también poliedros duales entre sí, si tomamos los puntos medios de las caras del octaedro obtenemos el cubo y en este caso la recíproca es cierta.
Tenemos entonces un poliedro compuesto,( figura 19) por dos poliedros regulares que son duales, por tanto tenemos un poliedro compuesto dual.
En la figura 9, 10, 11 y 12 se observan las perspectivas axonométricas isométricas de las Figuras 4, 5, 6 y 7, mientras que en la figura 8 tenemos dos vistas en planta y alzado del rombododecaedro, si tuviéramos el perfil podríamos comprobar que también tiene una vista exactamente igual a la planta y alzado.
En las Figuras 13, 14, 15, 16 y 17 tenemos otras perspectivas axonométricas pero trimétricas por tener ángulos desiguales, en la figura 20 tenemos la misma figura del poliedro compuesto del número 6 pero hemos marcado los puntos que definen el rombododecaedro, y los hemos unido mediante aristas de manera que vemos la relación entre la figura 6 y la figura 8, ya que este dibujo número 20 compromete a los dos, podemos verificar que esos puntos son los que se marcan en la figura 19. En el número 21 tenemos una perspectiva axonométrica isométrica de los dos prismas entrelazados correspondientes a la figura 1.
En el número 1 tenemos el icosidodecaedro que es la intersección del dodecaedro e icosaedro, números 5 y 6 respectivamente.
En el número 2 hemos cogido el icosidodecaedro en color amarillo - misma figura que la del número uno pero en un solo color- y le hemos añadido sobre las dos caras distintas (triángulo equilátero y pentágono regular) dos prismas rectos. Al prolongar las caras adyacentes tenemos planos que cortan a los prismas de manera que generan pirámides como en el número 3.
En el caso del prisma pentagonal las caras que prolongamos adyacentes son los 5 triángulos anejos, mientras que en el caso del prisma triangular prolongamos las 3 caras pentagonales regulares adyacentes.
El conjunto de los planos definen caras de pirámides que aparecen en el número 3 en color rojo y magenta.
Realmente si ahora añadimos todas esas pirámides a las caras obtendremos la figura número 7 que es la composición del dodecaedro e icosaedro, recíprocamente si al número 7 le quitamos las pirámides obtenemos el icosidodecaedro.
Si al número 7 le quitamos solo las pirámides verdes nos quedamos con el dodecaedro mientras que si al número 7 le quitamos solo las pirámides magentas nos quedamos con el icosaedro.
Como vemos los cuatro poliedros están íntimamente relacionados, el icosaedro y dodecaedro, número 6 y 5 por ser poliedros duales, la composición de los mismos que genera el poliedro compuesto número 7 qué es también un poliedro estrellado, y la intersección del número 5 y 6 del que obtiene el icosidodecaedro y que es exactamente el poliedro estrellado pero sin las pirámides.
En la figura número 3 tenemos un poliedro compuesto del dodecaedro que está en la figura 1 y del icosaedro que está en la figura 2. Las tres figuras están en sistema diédrico.
El dodecaedro e icosaedro son poliedros duales, si tomamos los puntos medios del dodecaedro obtenemos el icosaedro y recíprocamente si tomamos los puntos medios del icosaedro tenemos el dodecaedro.
Por tanto al hacer la composición de los dos tenemos un poliedro compuesto dual, la intersección de ambos poliedros genera un icosidodecaedro, que es un poliedro arquimediano formado por 12 pentágonos regulares y 20 triángulos equiláteros, es la figura que aparece en el número 8 en perspectiva axonométrica y el número 12 en sistema diédrico.
Si tomamos la figura 3 que es el poliedro compuesto y marcamos los puntos exteriores tal y como se ve marcados en la Figura 10, al pasar por los puntos caras de un poliedro obtenemos el triacontaedro rómbico que es un poliedro de Catalan y que aparece en la figura 11. Este procedimiento es lo que se llama la generación del poliedro mediante la envolvente convexa que consiste en coger los puntos externos del poliedro compuesto como hicimos en la Figura 10.
Si tomamos los dos poliedros icosaedro y dodecaedro del número 1 y 2, en perspectiva axonométrica los tenemos en el 4 y 5, al superponerlos obtenemos la unión de ambos poliedros que es el compuesto dual del dibujo de número 3 en diédrico, en perspectiva lo tenemos en el número 7.
Si al icosaedro le quitamos el dodecaedro nos queda la figura del número 6, una figura compuesta por numerosas pirámides de base pentagonal.
Si ahora hacemos el proceso contrario, del dodecaedro le quitamos el icosaedro obtenemos la figura del número 9 que está formada por pirámides de base triangular.
Cuando tomamos un poliedro compuesto y obtenemos la intersección de los dos poliedros decimos que es el núcleo del poliedro compuesto, en este caso ya vimos que era la intersección de ambos que es el icosidodecaedro, poliedro arquimediano que también lo podemos obtener al cortar ambos poliedros por los puntos medios de cada una de sus aristas, lo que se dice un corte de tipo 1.
Tomamos nuevamente el poliedro compuesto formado por el icosaedro y el dodecaedro de la figura anterior y su envolvente convexa que es el triacontaedro rómbico ( poliedro de Catalan).
En el número 1 tenemos las tres vistas en diédrico del triacontaedro rómbico, al igual que las otras dos figuras que mostramos en diédrico tienen la planta y el perfil exactamente iguales mientras que el alzado es también una proyección idéntica pero girada 90 grados.
Si cogemos la del número 2, es el rombicosidodecaedro (poliedro arquimediano) famoso por ser el balón de fútbol que ha sustituido al antiguo icosaedro truncado por tener más esfericidad.
Lo podemos obtener por ejemplo a partir de un dodecaedro al que le cortamos los vértices y las aristas, al achaflanar estos extremos obtenemos el poliedro arquimediano.
Por último en el número 3 tenemos el poliedro compuesto del dodecaedro e icosaedro (ambos poliedros regulares duales).
En la franja inferior encerrada en un rectángulo verde hemos puesto en el número 4 y 5 la proyección en planta del triacontaedro rómbico, en el 6 hemos puesto otra vez el rombicosidodecaedro y en el 7 el poliedro compuesto.
En el número 4 hemos marcado los vértices del triacontaedro rómbico, como podemos observar coinciden exactamente con los vértices salientes del poliedro compuesto del número 7, eso quiere decir que por cada uno de esos 4 puntos podemos hacer los rombos que definen el poliedro de Catalan, por cierto al igual que todos los poliedros de Catalan tendrá las caras exactamente iguales.
Si observamos el número 5 es realmente otra vez el triacontaedro rómbico del que hemos cogido los puntos medios de sus aristas, al unir sus puntos obtenemos las aristas del rombicosidodecaedro.
Podemos ver las estrechas coincidencias que hay entre tres poliedros de distintas clasificaciones.
viernes, 13 de noviembre de 2009
viernes, 6 de noviembre de 2009
Poliedros compuestos
Poliedros compuestos por giro y composición con otros poliedros
En la imagen inferior a la izquierda observamos perspectivas distintas de los tetraedros entrelazados y de la intersección de ambos a la derecha.
Al hacer el giro del cubo y dejar registro de 5 cubos podemos observar a su derecha en planta y alzado las cinco figuras que forman ese poliedro compuesto, a su derecha observamos la intersección, es un poliedro nuevo bastante curioso ya que la parte superior e inferior según vemos en el alzado son fragmentos de deltoedros, mientras que por la franja central y ecuatorial son trapezoides en zig-zag que suben y bajan en sus aristas cercanas a los paralelos de una imaginaria esfera próxima al poliedro.
A la derecha podemos observar dos perspectivas del poliedro compuesto y otras dos perspectivas de la intersección de los 5 cubos.
Podemos observar a su derecha el caso de 5 prismas que genera un poliedro compuesto y la intersección más a su derecha, una figura formada por triángulos escalenos, mientras que a la derecha del todo de la imagen observamos el caso de 6 prismas, como hay coincidencia entre caras según vemos en el alzado en vez de salir una figura con triángulos escalenos sale una figura formada por dos pirámides, lo que se llama una dipirámide, vemos por tanto que los triángulos que salen son isósceles.
En el borde inferior podemos ver varias perspectivas de las 4 figuras distintas, los dos poliedros compuestos y la intersección de los mismos.
Curiosamente en la figura 4 en planta aparece una vista con apariencia de octaedro truncado, figura que vemos en diédrico en el número 8, da la impresión de que en el 4, en la planta, está formado por un cuadrado y hexágonos regulares, al igual que el octaedro truncado, pero si bien el cuadrado es real y está en verdadera forma, los hexágonos son irregulares, por otro lado podemos comprobar entre la figura 4 y 8 que el alzado y el perfil no coinciden.
En la figura 5 aparecen los 3 poliedros en estructura alámbrica y la obtención de las distintas caras, podemos observar en la parte superior la intersección de ese conjunto de líneas rojas y verdes que producen el cuadrado, sobre cada cara se daría el mismo caso, y luego serían tres líneas que une cada uno de esos cuadrados con ángulos iguales, sin olvidar que el poliedro nuevo que sale y que tiene por contorno en perspectiva axonométrica isométrica un hexágono regular, es lo común a los tres poliedros, una figura formada por hexágonos irregulares, 4 en la parte superior, cuatro en la parte inferior y otros 4 en la parte lateral con lo cual tenemos 12 hexágonos irregulares, mientras que cuadrados tenemos uno en la cara superior y otra en la inferior y 4 laterales, en total 6 cuadrados, la figura la podemos ver en una axonometría trimétrica en el número 6 y podemos contrastarla con el número 9 que es el octaedro truncado, poliedro arquimediano formado a partir del octaedro regular y al que se le cortan las esquinas.
En el número 7 aparecen las vistas de los prismas en modelo alámbrico mientras que en la intersección aparece el poliedro con un modo sombreado a color.
Podemos observar en el número uno la figura en planta y alzado que se obtiene al girar el cubo de la figura 3 tomando como eje el que marca la figura, una línea que une puntos medios de aristas opuestas del cubo.
Como podemos observar en el número uno aparecen los 5 cubos de manera que el eje está en posición vertical, al hacer la intersección de los 5 cubos obtenemos la figura número 2 que está constituida por deltoedros y hexágonos irregulares en su franja ecuatorial, en la figura 4 podemos observar el poliedro compuesto y la intersección de los cubos, el primero en modelo alámbrico y el segundo en modelo sombreado a color, si bien en la planta queda perfectamente definido por donde se determinan los deltoides en el alzado; como resulta complejo determinar la posición de los deltoides se ha dibujado en la figura 5 las líneas que coinciden con las aristas del poliedro compuesto.
De la figura 6 a las 8 tenemos varias perspectivas del poliedro compuesto y la intersección de los 5 cubos.
En el número 4 observamos exactamente el mismo ejercicio pero ahora el eje en vez de ser una línea horizontal como pasaba en el ejercicio 1 ahora es una línea vertical, en consecuencia observamos en el número 5 la misma figura que teníamos en el número 2 pero con una visualización más intuitiva e inteligible, a su derecha en el número 6 observamos los tres cubos en modelo alámbrico mientras que la intersección de los tres cubos aparece con las caras planas a color para una mejor comprensión de la figura en diédrico.
De los números 8 al 12 podemos observar distintas perspectivas del poliedro compuesto y de la intersección de los tres cubos.
Como podemos observar en principio parece un deltoedro que se aproxima a un prisma oblicuo de manera que sus caras podrían ser rombos, romboides o deltoides
En el borde inferior izquierdo podemos observar ese mismo prisma oblicuo con las tres proyecciones en sistema diédrico.
En la parte inferior de la figura podemos observar ya varias perspectivas de ambas figuras, el poliedro compuesto y la intersección de las pirámides.
En el número 5 y 4 observamos dos perspectivas de esta figura de intersección mientras que en el 6 y 7 observamos el poliedro compuesto por los tres cubos.
Al hacer el giro y registro de tres cilindros observamos en la intersección el deltoedro de la imagen central. A su izquierda observamos los tres cilindros que forman una figura compuesta, mientras que en la parte inferior observamos la perspectiva de ambas figuras en axonometría.
En la parte inferior observamos dos proyecciones de la composición de cilindros y de la intersección de los mismos mientras que a la derecha observamos un alzado de la intersección de los 6 cilindros.
En el borde superior izquierdo de la imagen vemos una elipse atravesada por una recta secante, esa elipse es la proyección de un elipsoide de revolución que aparece en color azul inmediatamente debajo, con la recta que lo atraviesa por un plano meridiano.
Al hacer el giro del elipsoide respecto al eje y dejar el registro de 3 elipsoides obtenemos en planta y alzado la figura central de la imagen, a su derecha podemos observar las intersecciones.
Podemos hacer una analogía con los deltoedros pero imaginándolos con líneas curvas, de manera que entre los deltoedros aparecen formas poligonales, como análogamente sucedía al hacer un giro de un octaedro regular.
A la izquierda en el borde inferior observamos la composición de los elipsoides en perspectiva mientras que a su derecha observamos tres perspectivas de la intersección de los mismos.
En el número 3 y 4 observamos las perspectivas axonométricas de esta figura mientras que en la 5 y 6 observamos la composición de los siete prismas.
Esta figura número 2 es un prisma oblicuo, un caso particular del deltoedro de la figura anterior en la que los deltoides se convierten en rombos.
En el número 5 y 6 podemos observar la composición de los tres prismas mientras que en el 3 y 4 distintas perspectivas del deltoedro o si preferimos prisma oblicuo.
En el borde superior izquierdo de la imagen observamos un prisma hexagonal regular recto que es atravesado por un eje que lo atraviesa de una arista a otra opuesta.
Al hacer un giro respecto a ese eje y dejando registro de 5 figuras obtenemos la planta y alzado de la figura 1, la intersección de los 5 prismas es el deltoedro que aparece en el número 2.
En el número tres y cuatro tenemos nuevas perspectivas de los cinco prismas entrelazados mientras que en el 5 y 6 tenemos dos perspectivas distintas del deltoedro.
En las dos franjas inferiores podemos ver las perspectivas de esos cinco elementos y a la derecha el tetraedro original con su eje de giro.
En la parte inferior de la imagen podemos observar las perspectivas de ambas figuras.
En el borde superior derecho aparece en planta y alzado los dos tetraedros entrelazados y a su derecha la planta y alzado de la intersección de ambos que es el octaedro regular, debajo tenemos dos perspectivas del octaedro.
En el centro superior de la imagen observamos un cubo con varios colores, uno de ellos corresponde a una pirámide en amarillo. Si cortamos 4 trozos como ese del cubo podemos también obtener el tetraedro, en la imagen izquierda superior se observa el tetraedro rojo después de haber quitado esas 4 pirámides azules al cubo.
En el centro observamos nuevamente el tetraedro con el eje que lo atraviesa mientras que a la derecha o observamos la intersección de los 3 tetraedros que provoca el deltoedro representado en planta alzado y perfil, por debajo del perfil podemos obtener la imagen en axonometría isométrica del deltoedro.
En el centro observamos nuevamente el tetraedro con el eje que lo atraviesa mientras que a la derecha o observamos la intersección de los 3 tetraedros que provoca el deltoedro representado en planta alzado y perfil, por debajo del perfil podemos obtener la imagen en axonometría isométrica del deltoedro.
A la derecha obtenemos las mismas figuras del 2 al 5 qué equivalen del 2 al 5 en el otro grupo pero ahora los números aparecen en color azul, quiere decir que están representados en otra perspectiva. También tenemos en azul otra perspectiva conforme a la de los números azules anteriores donde aparecen las perspectivas de los cuatro poliedros, el 9 es un rombododecaedro.
Si ahora tomamos el rombododecaedro que es la figura que aparece en el número 10 y le cortamos las pirámides de base triangular en sus esquinas obtenemos el poliedro azul número 12 que es un octaedro regular, también podríamos cortar pirámides de base cuadrangular para obtener un cubo.
Podemos ver el truncamiento -aplicado sobre rombododecaedro- de las pirámides de base triangular en el número 11.
Los tres prismas entrelazados lo representamos en planta, alzado y perfil en el número 1 y según esa disposición tenemos en el número 2 la intersección de los 3 prismas en planta alzado y perfil.
Si tomamos la perspectiva axonométrica de los tres prismas entrelazados que es realmente lo que aparece en el número 3, obtenemos en la intersección la figura del rombododecaedro en perspectiva axonométrica isométrica en el número 4.
Si ahora tomamos el rombododecaedro dibujado en el número 8 en color verde y en el 9 de la misma manera, pero con modo alámbrico, observamos que al cortar pirámides de la figura obtenemos la figura número 10 que es el octaedro regular.
En la Figura 12 aparece el octaedro al que se le han quitado algunos trozos para empezar a construir el octaedro regular.
En la parte inferior de la imagen vemos a la izquierda las perspectivas de los cinco octaedros entrelazados a la izquierda, en el centro observamos las perspectivas de las pirámides, y a la derecha observamos el octaedro regular y la posición del eje sobre el cual se ha girado la figura para provocar 5 octaedros entrelazados y sus intersecciones.
A la derecha vemos un octaedro regular verde con el eje vertical que pasa por vértices opuestos, la distancia entre vértices opuestos es siempre la misma por cierto.
Al girar el octaedro regular y dejar registro de tres octaedros podemos observar la figura resultante en el borde inferior izquierdo en sistema diédrico, planta, alzado y perfil de los tres octaedros y debajo del perfil la perspectiva de ese conjunto de poliedros.
A la derecha podemos observar la intersección de todos estos octaedros regulares, como podemos observar es una dipirámide que aparece en planta, alzado y perfil.
Más arriba se puede ver en sistema diédrico ambas figuras, a la izquierda los dos tetraedros regulares entrelazados y a la derecha la intersección de los mismos.
En la imagen del centro podemos ver un octaedro regular que se gira en torno al eje que tiene marcado entre los puntos medios de dos aristas opuestas, una vez que se hace el giro se deja el registro de 7 octaedros, de manera que obtenemos la representación en planta y alzado que tenemos en la izquierda, se ha hecho también una vista auxiliar para mostrar las formas estrelladas en verdadera forma.
A la derecha del dibujo aparece la intersección de todos esos octaedros regulares, en la parte inferior de la imagen aparecen las perspectivas, a la izquierda del conjunto de poliedros y a la derecha del poliedro resultante de la intersección de todos.
Una vez que se gira la figura en torno a ese eje se deja en registro de cinco dodecaedros.
En la figura 1 de la izquierda superior aparece en planta y alzado los cinco dodecaedros que se forman, a su derecha en el punto 2 aparece la intersección de esos cinco dodecaedros.
En el número 3 observamos la misma figura de cinco dodecaedros superpuesto a otros cinco girados también pero tras haber aplicado a estos últimos un giro de 90 grados, en la figura 4 podemos ver la intersección de esos 10 dodecaedros.
En la parte inferior de la imagen podemos observar las perspectivas de los cuatro ejercicios distintos.
Podemos ver en la figura 2 3 4 y 5 la superposición de los tres prismas en el primer caso y de dos prismas en los casos 3 4 y 5
Tenemos en el número 6 la intersección de los 3 prismas que corresponde a la figura 2, como podemos ver es un dodecaedro irregular, una figura de 12 caras que tiene polígonos pentagonales irregulares. Esta figura es una composición de las intersecciones 7 8 y 9, que son respectivamente las intersecciones de los prismas de las figuras 3, 4 y 5.
En la Figura 12 puedes ver la estructura de las figuras 7 8 y 9 superpuestas en modo alámbrico mientras que en color aparecen la intersección de las 3, así como en el poliedro de la figura 6.
En la Figura 11 vemos también las formas alambricas de las formas 7 8 y 9, mientras que en la Figura 14 le cortamos las esquinas piramidales a la 13 y obtenemos la figura 15 que es el icosaedro regular.
En los casos 1 2 y 3 son las intersecciones de los prismas anteriores pero en conjunto de dos prismas, podemos ver que las tres figuras son idénticas pero están dispuestas en formas distintas de manera que si juntamos todas obtenemos la figura que sale en el borde superior derecho de la imagen.
En el borde inferior derecho de la imagen aparece la intersección de esos tres bloques, los tres en estructura alámbrica y la intersección de los mismos a color, que es un dodecaedro regular.
A la derecha obtenemos la perspectiva de la figura, como podemos observar es un poliedro con bastante esfericidad formado por un hexágono irregular que está rodeado siempre de pentágonos irregulares, de esta manera obtenemos tres franjas de pentágonos irregulares que siguen meridianos de la esfera que lo inscribe. siendo esas tres franjas incidentes por los planos coordenados y dejando los hexágonos ubicados entre las tres franjas de pentágonos.
En la parte inferior de la imagen podemos observar las cuatro perspectivas de los poliedros en cuestión.
En la fila inferior se muestran los cuatro poliedros en perspectiva.
A la derecha observamos en planta, alzado y en perspectiva el resultado de aplicar la intersección que describimos al principio.
Podemos observar en esta imagen el mismo caso que el anterior, el eje de giro es la diagonal principal y al dejar registro de 5 cubos obtenemos el deltoedro que se observa en la parte izquierda de la figura mientras que a la derecha el registro de 4 cubos y sus intersecciones genera una figura formada por dos pirámides llamada dipirámide.
A la izquierda de la imagen en su parte superior podemos observar un icosidodecaedro.
A su derecha podemos observar un icosidodecaedro y un dodecaedro superpuestos generando un poliedro compuesto, esa figura aparece a la derecha de esta pero ahora en una perspectiva, al aplicar la intersección de esos los poliedros regulares obtenemos la imagen en el borde superior derecho de un icosidodecaedro, realmente es el volumen común a los dos poliedros anteriores.
Más abajo podemos observar que un dodecaedro a la izquierda más un icosaedro se intersecan provocando esa figura que está señalada con una flecha, abajo a la izquierda podemos observar el poliedro compuesto por ambos poliedros, icosidodecaedro y dodecaedro y abajo de todo a su derecha observamos la perspectiva de la intersección de ambas figuras.
Podemos observar también a la derecha en la parte inferior un poliedro compuesto en planta y alzado y a su derecha una perspectiva, en el borde inferior derecho aparece dentro de una elipse las dos figuras objeto de la composición e intersección, el dodecaedro y el icosidodecaedro.
La intersección de esos tres prismas provoca un dodecaedro irregular del que podemos cortar sus esquinas provocando un icosaedro regular.
Paradójicamente si hacemos lo mismo con su poliedro dual, el dodecaedro regular, en las intersecciones de sus tres prismas construidos con los contornos nos da realmente el dodecaedro regular. Siendo duales ambos poliedros y teniendo tantas coincidencias al igual que el dodecaedro genera en sus vistas convertidas en prismas el mismo poliedro, parecería normal que el icosaedro también provocara directamente la misma figura pero no es así, hay que truncarlo para obtener otra vez el icosaedro regular.
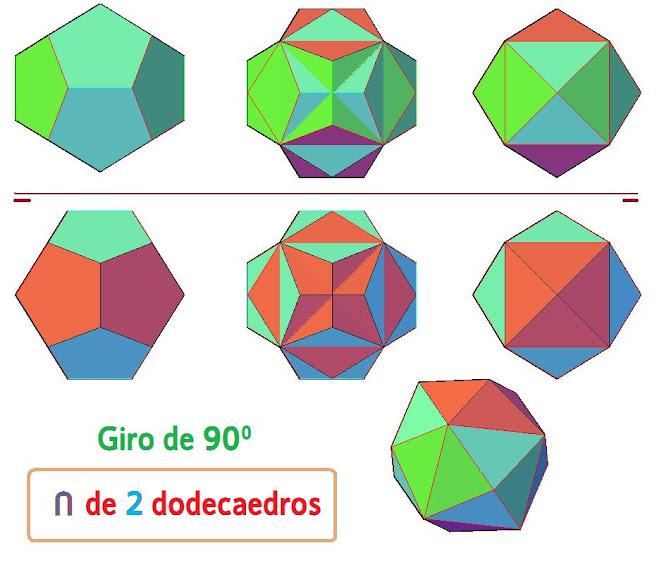
En la imagen podemos ver en planta y alzado y a la izquierda un dodecaedro regular, poliedro formado por 12 caras pentagonales regulares, del mismo poliedro se hace una copia y se gira 90 grados horizontalmente obteniendo en la superposición con el poliedro anterior un poliedro compuesto que aparece en planta y alzado en el centro de la figura. A la derecha podemos observar la intersección de ambos poliedros, como podemos observar realmente es un cubo que tiene apoyadas en sus caras pirámides, es muy parecido a un poliedro de Catalan que tiene aproximadamente la misma forma aunque la inclinación de las caras difiere un poco, es llamado hexaedro tetrakis, dual del arquimediano llamado octaedro truncado y que se obtiene al cortar las caras del octaedro regular por un corte de tipo 2 de manera que cada cara triangular provoca un hexágono regular rodeado de cuadrados. Si tomamos los centros de las caras de este poliedro de Catalan obtenemos el arquimediano octaedro truncado.En la imagen podemos observar a la izquierda en planta y alzado un poliedro compuesto por 2 dodecaedros regulares, el eje de giro que provoca estos dos poliedros se puede ver en la parte derecha de la imagen, el dodecaedro regular original es girado por un eje que es una recta horizontal que pasa por una diagonal de la figura interceptando a los dos vértices de la figura que se ven en planta. Al hacer el registro del giro obtenemos el poliedro compuesto cuya intersección aparece en el centro de la imagen en planta y alzado, podemos observar que es la composición de dos pirámides en los extremos y otras pirámides truncadas unidas por la base y cuyas caras laterales son trapecios.
En el borde inferior derecho esa misma figura formada por 3 cubos se coge y se gira 90 grados, sin borrar la anterior se superpone a la misma y se obtiene la intersección de 6 cubos, en la parte central inferior de la figura podemos observar en planta y alzado el resultado de la intersección de esos 6 cubos, realmente es la intersección de dos prismas, de manera que tienen los ejes ortogonales entre sí.
En la imagen podemos observar el ejercicio que ya vimos en los casos anteriores, el 76, el 77 y el 80, el cubo que era girado a través de un eje que pasaba por la mitad de sus aristas provocando esa figura que ahora aparece en distintas posiciones, en el lado izquierdo observamos que el cubo amarillo aparece con sus proyecciones en planta y alzado representadas como un cuadrado, observamos que el eje de giro es una línea de perfil qué pasa a 45 grados por la mitad de las aristas de ese cubo provocando en consecuencia una intersección que aparece con el eje inclinado en el mismo grado según se ve a su derecha.
En el lado derecho podemos observar que ahora el eje de giro es una recta horizontal qué forma 45 grados con el plano vertical de esta manera la intersección aparece en una forma más inteligible.
Aquí tenemos el caso 6 de la figura 77, podemos observar que el eje en planta y alzado tal y como aparece a la izquierda de la imagen pasa por los puntos medios de las aristas verticales del cubo amarillo, al hacer el giro de este cubo en una vuelta completa y dejando registro de 3 cubos a 120 grados podemos observar cómo se genera una figura formada por pirámides en sus partes opuestas, o sea una dipirámide, que es cortada por un prisma hexagonal, el tipo de corte hace que provoque en las pirámides caras de deltoides y en el prisma caras
Hacemos la misma transformación que en el ejercicio anterior, pero en este caso tomamos un icosaedro y tomando dos aristas opuestas respecto al centro de la figura obtenemos un eje sobre el que giramos la figura dejando registro de tres icosaedros, las proyecciones de estas tres figuras aparecen en el centro de la imagen mientras que a la derecha aparece la intersección de las tres figuras, como en el ejercicio anterior en la parte inferior de la imagen obtenemos varias perspectivas de ambas configuraciones.
Volvemos a tomar el icosaedro pero ahora colocamos el eje de giro por dos vértices opuestos del mismo, tal y como se ve a la derecha de la imagen, al girar la figura y dejar el registro de 2 icosaedros obtenemos el poliedro compuesto cuyas proyecciones en planta y alzado aparecen a la izquierda de la imagen, a su derecha y en el centro de la imagen podemos observar la intersección de los dos icosaedros en planta y alzado.
Podemos observar a la izquierda las proyecciones en planta y alzado del dodecaedro, tenemos una recta de punta que atraviesa el dodecaedro por la mitad de dos aristas opuestas, esta recta que corta la figura es el eje de giro que provoca según se ve en el centro de la imagen la composición de 3 dodecaedros girados cada uno respecto al anterior a 120 grados, a su derecha podemos observar la intersección de los 3 poliedros regulares y más a la derecha observamos las perspectivas de los tres dodecaedros entrelazados mientras que en la parte inferior de la imagen podemos observar las perspectivas axonométricas de la intersección de los 3 poliedros.
A la izquierda de la imagen podemos observar el icosidodecaedro, es la figura intersección del dodecaedro e icosaedro, poliedro arquimediano que también se puede obtener por el truncamiento de tipo uno de los poliedros anteriores. Cogemos un eje de giro que pasa por vértices opuestos y giramos la figura de manera que dejamos registro de 5 icosidodecaedros, de esta manera obtenemos en planta y alzado las proyecciones de esas figuras. Esas dos proyecciones las podemos ver en el centro de la imagen mientras que a su derecha podemos observar la intersección de esos cinco poliedros, una figura formada por trapecios, hexágonos y deltoides.
Tenemos en el borde superior izquierdo un dodecaedro que como vemos en la parte inferior es girado por dos ejes de giro, uno que corresponde al eje A y otro que corresponde al eje B, al hacer el giro de 5 elementos obtenemos la figura que aparece en el Centro de la Imagen en sus proyecciones en planta y alzado mientras que al hacer el giro respecto al otro eje e interfiriendo la misma figura que sale con el poliedro anterior obtenido, obtenemos a la derecha de la imagen la intersección de aplicar los dos giros. tenemos en el primer caso que es la intersección de 5 dodecaedros y esa misma figura también la hemos obtenido mediante un giro de un eje ortogonal al anterior, de manera que la intersección del giro de A + B es en realidad la intersección de 10 poliedros.El poliedro obtenido al final resulta de la intersección los cinco dodecaedros girados respecto a un eje y los otros cinco dodecaedros girados respecto al otro eje ortogonal.
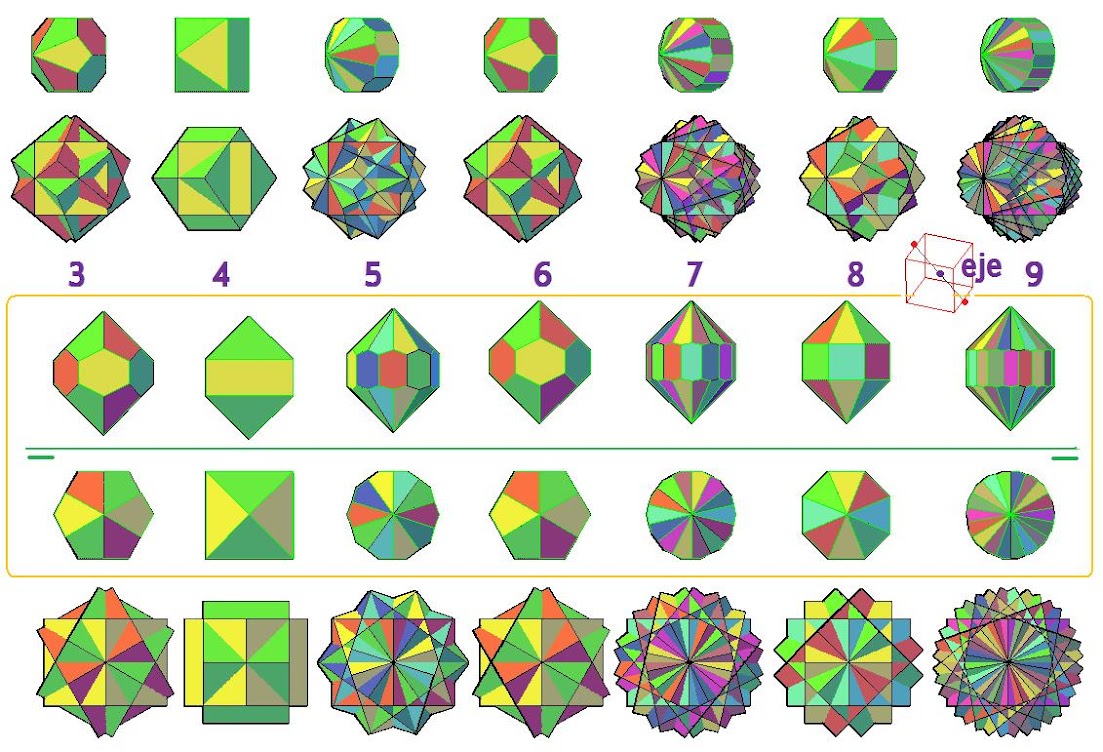
Un cubo gira tomando como eje el segmento que pasa por el centro de aristas opuestas, tal y como se ve en el centro de la imagen. Una vez que gira el cubo va dejando registros de 3 cubos, cuatro, cinco... y así hasta nueve. Podemos ver en la parte inferior de la imagen las distintas perspectivas de los cubos entrelazados y justo por encima una franja con el poliedro resultante de la intersección de todos esos cubos girados. En el caso de cuatro cubos se da la misma situación que con dos cubos ya que son coincidentes tras el giro y es como si hubiera solo dos cubos.
En la franja horizontal superior observamos las proyecciones ortogonales de las intersecciones de esos cubos mientras que en la franja inferior observamos todos los cubos entrelazados desde el 3 hasta el 9.
Podemos observar en el caso 3, 5, 6, 7 y 9 que obtenemos poliedros formados por deltoides y hexágonos mientras que en el caso 4 y 8 obtenemos poliedros formados por triángulos y rectángulos.
A la derecha de estas dos vistas en planta y alzado obtenemos las dos vistas correspondientes de la intersección de todos los cubos, como podemos observar es una dipirámide, una figura formada por dos pirámides unidas por sus bases, a su derecha hemos cogido la misma figura y la hemos girado 90 grados, superponiéndola a la anterior obtenemos las dos dipiramides unidas en una sola configuración poliédrica, a la derecha obtenemos la intersección de esas dos formas, como vemos es una estructura poliédrica muy caprichosa llena de polígonos irregulares pero con bastantes simetrías pese a la transformación, en el borde inferior derecho podemos ver la perspectiva de cada una de las configuraciones que hemos ido haciendo, de izquierda a derecha podemos ver en perspectiva axonométrica los cuatro cubos girados en torno al eje, la dipirámide resultado de la intersección de los cubos anteriores, el producto de incorporar las dos pirámides de manera que una está girada 90º y por último la intersección de estas dos últimas figuras.
Como podemos observar en la imagen del borde inferior izquierdo ahora hemos cogido un cubo y hemos tomado como eje una línea que pasa por el centro de aristas opuestas, al girar ese cubo los 360° obtenemos 4 cubos de los que dejamos registro obteniendo en planta y alzado la figura que se ve formada por los 4 cubos entrelazados, como podemos observar a su derecha la intersección de estos cuatro cubos es un poliedro formado por dos pirámides unidas en sus bases por un prisma recto cuyas caras laterales son rectángulos.A la derecha podemos observar la misma figura de manera que el cubo rojo nos muestra en planta una arista superior en posición horizontal, de esta manera a la derecha podemos observar más clara la intersección de los 4 cubos donde efectivamente se ven las dos pirámides y el prisma que en las enlaza.
Curiosamente en la figura 60 teníamos la misma disposición para el eje de giro, pasaba también por el centro de dos aristas opuestas pero como se dejaba el registro de 3 cubos obteníamos una figura formada por deltoides y hexágonos laterales, mientras que en este caso en vez de deltoides son triángulos y en vez de hexágonos laterales son rectángulos. Cuando las caras superior e inferior de la pirámide aparecen paralelas obtenemos rectángulos laterales como en este caso, mientras que cuando las caras están ligeramente giradas como pasa en el ejemplo de los tres cubos obtenemos figuras alternas que provocan los deltoides y los hexágonos irregulares.
Podemos observar en el borde superior derecho la planta y alzado de la intersección de los 5 dodecaedros, es una figura formada por deltoides en la parte inferior y posterior y por hexágonos irregulares a lo largo de la parte central de la figura. Podemos observar también en axonometría la representación de esta figura en el borde inferior derecho.
En la parte superior derecha vemos más de cerca los cuatro cubos con sus respectivas intersecciones mientras que en el centro superior de la figura aparece un cubo en planta y alzado en color amarillo y azul en el se marca la posición del eje de giro, un eje de giro que coincide con la diagonal principal del cubo y que es el que sirve para generar la figura de unión e intersección de los 4 cubos tal y como los vimos en el borde inferior central y derecho de la figura.
En la parte superior izquierda de la figura aparecen otra vez los cuatro cubos unidos pero de manera que el eje de giro coincide con la figura del cubo en amarillo y azul por eso aparece en posición oblicua, es realmente la misma figura del borde inferior central pero en posición oblicua.
Al practicar el mismo ejercicio pero en vez de utilizar 6 prismas utilizando solo tres obtenemos la figura que aparece a la derecha con los tres prismas azul verde y rojo, como podemos observar la intersección está formada por una figura distinta a la obtenida en el caso anterior, ésta está formada por caras triangulares de manera que los vértices laterales de la figura alternan a distintas alturas, no como en el caso de la dipirámide anterior.
Cuando cogemos los tres prismas según las tres direcciones ortogonales y practicamos la intersección de los mismos obtenemos un dodecaedro irregular tal y como vemos en la parte inferior de la imagen.
En la parte derecha de la imagen vemos las proyecciones del icosaedro regular en color azul, el dodecaedro regular en color dorado y en la parte inferior derecha vistas y proyecciones auxiliares del icosaedro regular en color plateado.
En esta figura podemos observar la composición de dos cubos, en este caso el eje de giro es una línea que pasa por la mitad de sus aristas y a la que se ha aplicado un giro de 90 grados. Como podemos observar la figura que sale es una pirámide que se ha separado de manera que se intercala un prisma recto en el medio, esto es, una figura formada por dos pirámides y un prisma.
Si cogemos y giramos un cubo dejando un registro de 7 cubos y la intersección de los mismos obtendremos el deltoedro que se ve a la derecha en planta y alzado. Esta figura está formada por la intersección de esos 7 cubos generados a partir del giro de 1 de ellos y en ángulos iguales.
En la parte izquierda podemos observar los 7 cubos sin que todavía se haya aplicado la intersección.
Podemos ver el mismo caso que el anterior pero aplicado a 5 cubos al girar un cubo sobre su diagonal principal obtenemos esas proyecciones de los cubos que aparecen en su totalidad en el borde superior izquierdo mientras que en la parte central superior de la figura aparece ya el deltoedro en sus vistas como intersección de los cubos. Podemos verlo más de cerca a la derecha y en la parte inferior observamos lo mismo pero los figuras están dispuestas mediante un giro para que se vean en una proyección más intuitiva y fácil de entender.
Podemos observar otra vez el mismo ejercicio pero una ampliación de la imagen central de la figura con todos los cubos girados y sus intersecciones nos delimitan ahí la posición exacta de toda esa configuración que en su intersección define un deltoedro.